十五、三维圆柱状螺旋时空方程

设想在某处空间区域里存在着一个质点o点，相对于我们观测者静止，以o点为原点，建立一个三维笛卡尔直角坐标系x,y,z。

在时刻t’= 0，考察物体o点周围空间中任意一个空间点p，其位置我们用 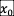， ， 来表示，由o点指向p点的空间位移失径【简称位矢】我们用 来表示。

p点运动经历了一段时间t后，在t”时刻到达p点后来所在的位置x, y, z ，由o点指向p点的空间位移失径【简称位矢】我们用 表示，有时空同一化方程：

简写为：

标量形式：

r是矢量 的数量。

相应的有三维螺旋时空方程：

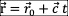
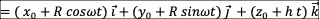
十六、质量和引力场的定义方程

统一场论中，物体o点的质量m，表示了o点周围立体角Ω=4π内以光速、以圆柱状螺旋式发散运动空间位移 的条数n。

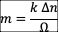
微分式为：

o点在周围空间p点产生的引力场 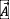，表示了穿过包围o点的高斯球面s =4πr²上【p点落在s上】，以光速发散运动的空间位移的条数n。

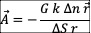
G是万有引力常数，k是比例常数，r是由o点指向p点的矢径 的数量，△S是高斯球面s中一小块，△n是数目。

十七、空间的运动具有波动性。

∂²/∂x² + ∂²/∂y² +∂²/∂z² = （∂²/∂t²)/c².

▽² = （∂²/∂t²）/ c².

是由质点o指向空间中考察点p点的矢径 。

十八、场的定义。

相对于我们观察者，由质点指向周围空间中任意一个空间点的位移矢量随空间位置变化或者随时间变化，这样的空间称为场，也可以叫物理力场。

不同的场是空间位移量关于空间位置的导数或者关于时间的导数所表现出的不同运动程度。

由于场的实质是【相对于我们观察者】空间本身运动的位移量关于时间和空间位置的导数，我们可以说在某一个立体范围内空间的运动量是多少，某一个平面内空间的运动量是多少，某一个曲线内空间运动的运动量是多少。这样，相应的场有三种形式：

1，场在三维立体上的分布。

2，场在二维曲面上的分布。

3，场在一维曲线上的分布。

场论高斯散度定理刻画了三维立体空间里场分布和二维曲面上场分布之间的关系。

斯托克斯定理刻画了场在二维曲面上的分布和场在一维曲线上的分布之间的关系。

场论梯度定理刻画了场在三维立体空间里的分布和场在一维曲线上分布之间的关系。

十九、电荷与电场的定义方程

在统一场论中，质点o如果带有电荷q，q表示单位时间里、单位立体角上穿过的 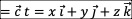的条数。也就是质量m随时间t变化的变化程度就是电荷，所以，有电荷的定义方程：

式中k和k’为常数。

以上就是电荷的微分定义方程。

静止电荷q产生的静电场 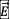的几何定义方程：

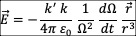
电场表示为单位时间里空间位移 穿过高斯球面s，在s上分布的密度，比起引力场就是多了时间因素。

二十、正负电荷模型

粒子带有正电荷在周围产生正电场，是由于粒子周围空间以圆柱状螺旋式、以光速向四周发散运动造成的。

正电荷.png

粒子带有负电荷在周围产生负电场，是由于粒子周围空间从无限远处以圆柱状螺旋式、以光速向电荷粒子汇聚运动造成的。

负电荷.png

正负电荷周围空间都是右手螺旋。

二十一、磁场的定义方程

设想在惯性参照系s’系里，一个相对于我们观察者静止的o点，质量为m’【以速度 运动时候为m】，带有正电荷q，在周围空间p【p点可以看成是空间点，也可以看成是场点、考察点】处产生了静电场 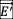，【如果是负电荷，加一个负号，以速度 运动时候为 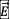】，由o点指向p点的矢径为 【以速度 运动时候为 】。

我们以 ’的长度r’【以速度 运动时候为r】为半径作一个高斯面s’ = 4πr’²包围o点。

在惯性参照系s系里，当o点相对于我们以匀速度 沿x轴直线运动的时候，可以引起 垂直方向电场的变化，变化的部分我们可以认为就是磁场 ：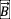

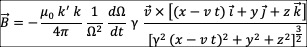
利用质量和电荷之间的关系 ，可以得到含质量的磁场定义方程：

二十二、随时间变化的引力场产生电场

o点运动时候，运动电场 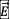和运动引力场 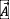之间满足的关系：

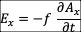
物体粒子静止和匀速直线运动的时候，电场和引力场之间的关系式是一样的。

二十三、匀速直线运动物体的引力场变化产生电场

f是常数，上式表示变化的引力场A可以产生电场E，也可以产生磁场B。

二十四，磁矢势就是引力场

引力场 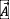的旋度和磁场 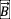所满足的关系：

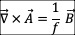
二十五、随时间变化的磁场B产生漩涡电场E和引力场漩涡A

当电荷o点相对于我们以加速度 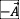沿x轴正方向运动，电荷o在周围任意一个空间点p处的磁场B发生变化，产生漩涡电场E和引力场 =

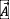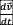
二十六、核力场的定义方程

所有的场都可以通过引力场变化而得到。核力场和电磁场一样也可以用引力场的变化来表示。

电场是引力场中的质量随时间变化而产生的，核力场所不同的是引力场中空间点的位置矢量 【模为r】随时间变化而产生的。

引力场

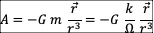
中的 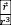随时间t变化，产生了核力场：

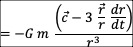
以上的 是矢量光速。

二十七、统一场论动量公式

物体静止时候周围空间以矢量光速C运动，因而具有静止动量P’ = m’C，标量为：p’ = m’c

物体以速度V运动的时候，运动动量P = m（C- V）

标量式为：

P = mc√（1-v²/c²）= p’ = m’c

二十八、力的定义。

力是物体在空间中运动状态或者物体周围空间本身的运动状态的改变程度。

二十九、统一场论动力学方程。

F = dP/dt = Cdm/dt - Vdm/dt +mdC/dt-mdV/dt

(C-V)dm/dt为加质量力， Cdm/dt 是电场力，Vdm/dt是磁场力，mdV/dt牛顿惯性力，也是万有引力，mdC/dt 是核力。

三十、能量的定义：

能量是物体在空间中【相当于我们观察者】运动程度或者物体周围空间本身运动的运动程度。

统一场论能量方程

m’c ² = mc ²√（1-v²/c²）

m’c²为o点静止能量，

o点相对于我们以速度v运动能量为 mc ²√（1-v²/c²）

其中mc² - Ek = m’c ², Ek ≈（1/2）mv²为动能。

三十一、光子模型。

光是加速运动的负电荷产生了反引力场，抵消了附近【或者自身】电子的静止质量，电子静止质量消失处于激发状态，静止在空间中【空间时刻光速运动】以光速运动。

电子受到了加质量的力F = C dm/dt（电场力）- V dm/dt（磁场力）的作用而质量消失，处以激发状态已光速运动。C是矢量光速，V是电子的运动速度。

运动光子的动量P = m C

m是光子运动质量，C是矢量光速。

运动光子的能量为mc ²

光子模型一种是两个激发电子绕一个轴线旋转运动，又在旋转平面的垂直方向上以光速运动。

一种单个激发电子以柱状螺旋式在运动。

光的粒子性是因为光子是激发电子，波动性是因为光子静止在空间中随空间波动而运动，光的波动性是因为空间本身的波动。

三十二、外星人飞碟飞行原理：

宇宙中任何物体如果你使它的质量变成零，这个物体就一定的突然以光速运动。

三十三、统一场论的主要应用。

1、造出可以光速飞行外星飞碟来

2、可以大规模使用冷焊的人工场

3，可以彻底治疗任何疾病的人工信息场

4、瞬间消失运动—-全球运动网

5、全球大规模无导线导电

6、汇聚太阳能接收器

7，无限压缩空间处理信息

8，时空冰箱。

9，虚拟建筑和虚拟人体。

10，场扫描记录人头脑内部意识信息，可以实现人脑和电脑的对接。